作业1 MVP投影变换

21 Nov 2022 2137字 8分
CC BY 4.0 （除特别声明或转载文章外）
如果这篇博客帮助到你，可以请我喝一杯咖啡~

作业1简单介绍

作业1简单介绍就是用三个点利用MVP在屏幕上画一个三角形。 Model transformation (placing objects)：模型变换，相当于是把物体摆好，把物体的坐标转化到世界坐标。 View transformation (placing camera)：视口变换，相当于把相机摆好，把坐标从世界坐标系转化为相机坐标系。 Projection transformation：投影变换，有正交投影和透视投影。 1

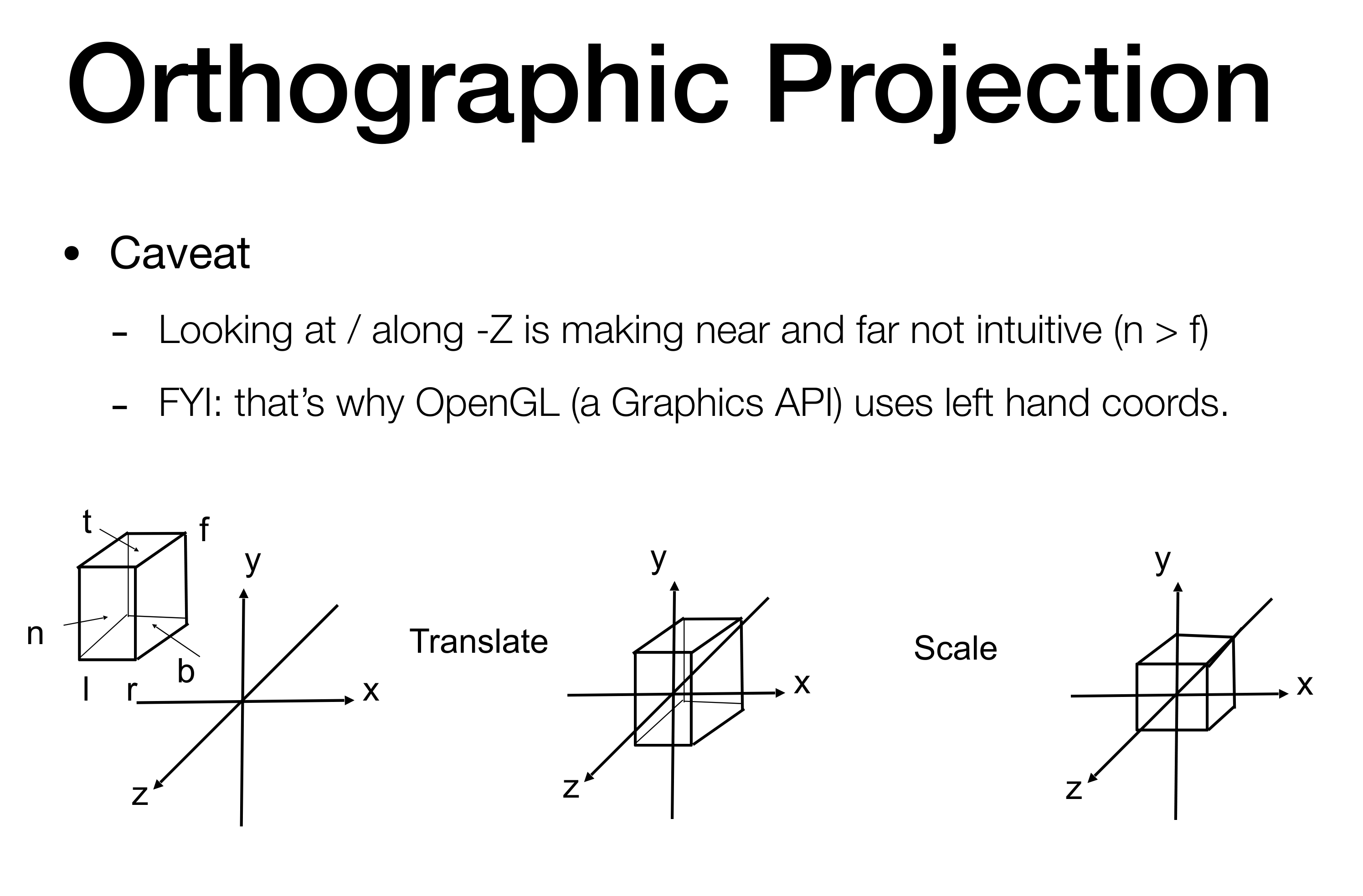
正交投影就是把中心点先平移到世界坐标中心，然后再放缩到 $[-1,1]^3$ 内

2

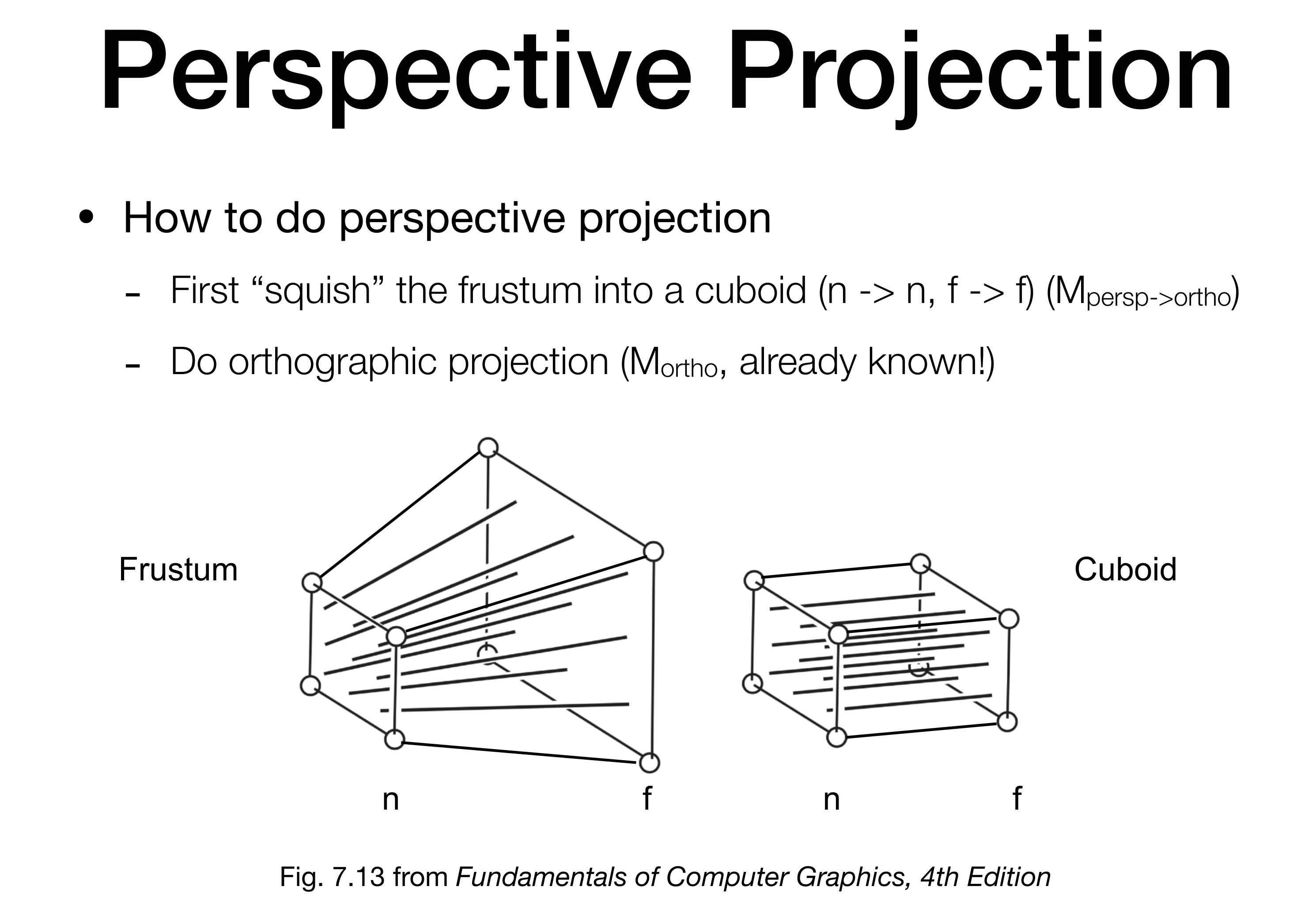
透视投影在正交投影的基础上进行一个挤压操作，然后再做正交投影。

先做挤压，再做平移，最后放缩。

基础变换

基础变换有旋转、缩放、切变、平移。

绕任意轴旋转

Rodrigues’ Rotation Formula：

\[\mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha)\left(\begin{array}{ccc} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{array}\right)\]

code

Eigen::Matrix4f get_rotation(Vector3f axis,float angle);
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.
    // float angle = rotation_angle/180.0f*MY_PI;
    // float c = cosf(angle),s = sinf(angle);
    // model << c,-s,0,0,
    //         s,c,0,0,
    //         0,0,1,0,
    //         0,0,0,1;
    Eigen::Vector3f axis;
    axis << 1,1,1;
    model = get_rotation(axis,rotation_angle);
    return model;
}

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar)
{
    // Students will implement this function

    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the projection matrix for the given parameters.
    // Then return it.
    Eigen::Matrix4f Mtrans,Mscale,Mp_to_or;
    float fovY = eye_fov*MY_PI/180.0;
    float t = abs(zNear)*tanf(fovY/2.0);
    float r = aspect_ratio*t;
    Mtrans << 1,0,0,0,
                0,1,0,0,
                0,0,1,-(zFar+zNear)/2.0,
                0,0,0,1;
    Mscale << 1/r,0,0,0,
                0,1/t,0,0,
                0,0,2.0/(zNear-zFar),0,
                0,0,0,1;
    Mp_to_or << zNear,0,0,0,
                0,zNear,0,0,
                0,0,zFar+zNear,-zFar*zNear,
                0,0,1,0;
    projection = Mscale*Mtrans*Mp_to_or;
    return projection;
}

Eigen::Matrix4f get_rotation(Vector3f axis,float angle){
    float fangle = angle*MY_PI/180.0;
    Eigen::Matrix4f I = Eigen::Matrix4f::Identity();
    Eigen::Matrix4f N,Rod ;
    Eigen::Vector4f axi;
    Eigen::RowVector4f taxi;
    axi << axis.x(),axis.y(),axis.z(),0;
    taxi << axis.x(),axis.y(),axis.z(),0;
    N << 0,-axis.z(),axis.y(),0,
        axis.z(),0,-axis.x(),0,
        -axis.y(),axis.x(),0,0,
        0,0,0,1;
    Rod = cosf(fangle)*I + (1-cosf(fangle))*axi*taxi + sinf(fangle)*N;
    Rod(3,3) = 1;
    return Rod; 
}