CC BY 4.0 (除特别声明或转载文章外)
作业4简单介绍
作业4 Bézier 曲线
 作业4 是实现 Bézier曲线,框架里其实已经给你实现了,这里你需要用它给的算法来实现
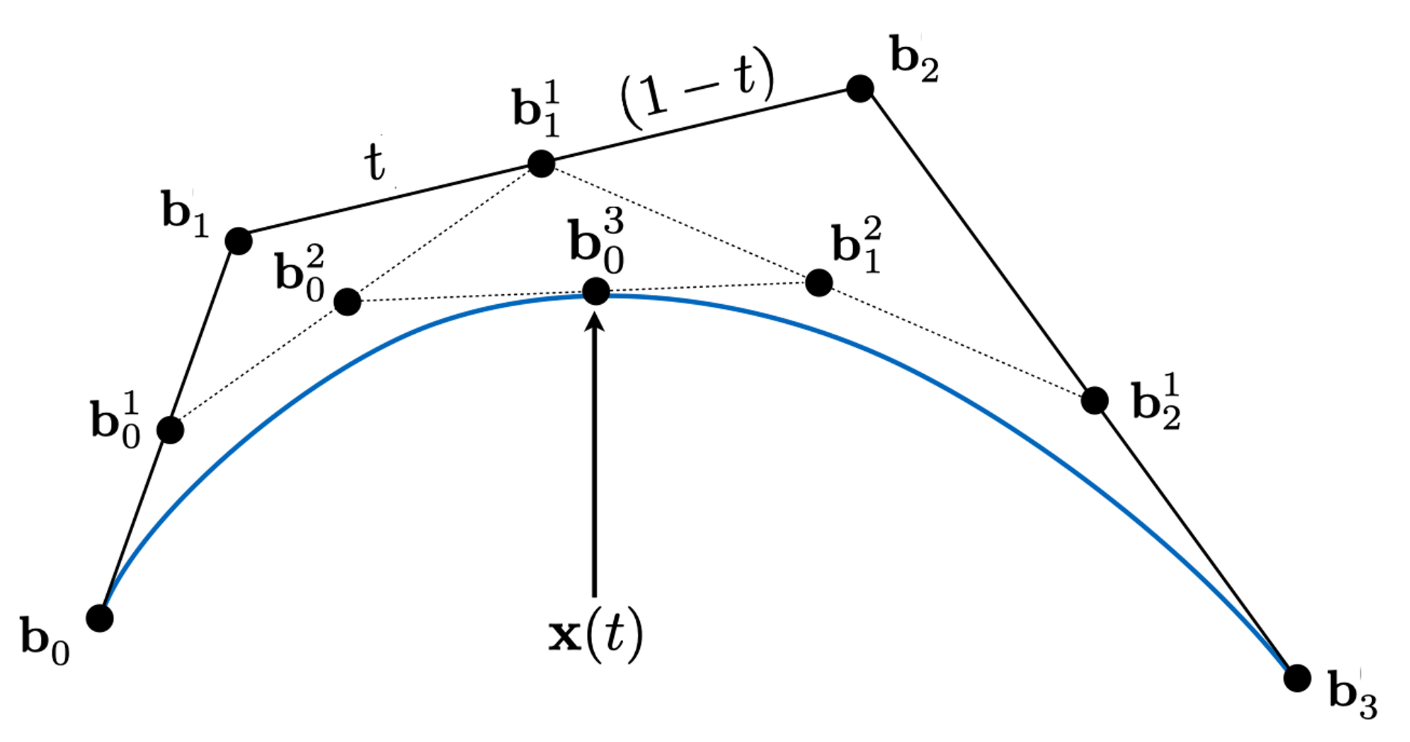
具体算法为:
作业4 是实现 Bézier曲线,框架里其实已经给你实现了,这里你需要用它给的算法来实现
具体算法为:

另外
为了让我们的曲线看起来光滑,我们需要进行抗锯齿处理。具体方法是把相邻的8个像素格子进行插值。虽然我们是在像素点中心进行计算,但是 $3*3$ 的像素,对角线的长度确实 $3\sqrt2$ , 所以距离应该是 $[0,\frac{3\sqrt2}{2}]$ ,然后转化为radio应该是 $radio=1-\frac{\sqrt2}{3}d$ ,最后还有记得取fmax。因为有可能这个像素点不止一次被用到。
code:
cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t)
{
// TODO: Implement de Casteljau's algorithm
if(control_points.size()==2) {
return (1-t)*control_points[0]+t*control_points[1];
}
std::vector<cv::Point2f> control_points_tmp;
for(int i = 0;i<control_points.size()-1;++i) {
control_points_tmp.push_back((1-t)*control_points[i]+t*control_points[i+1]);
}
return recursive_bezier(control_points_tmp,t);
}
void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
for(float t = 0;t <= 1;t+=0.0001) {
cv::Point2f point = recursive_bezier(control_points,t);
window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
for(int i=-1;i<=1;i++) {
for(int j=-1;j<=1;j++) {
if(point.x+i<0||point.x+i>700||point.y+i<0||point.y+i>700) {
continue;
}
float d = sqrt(pow(point.x-int(point.x+i)-0.5,2)+pow(point.y-int(point.y+j)-0.5,2));
float radio = 1.0 - sqrt(2.0)*d/3.0;
window.at<cv::Vec3b>(point.y+j, point.x+i)[1] = std::fmax(radio*255,window.at<cv::Vec3b>(point.y+j, point.x+i)[1]);
}
}
}
}
